Oka and uma: Difference between revisions
m (→Shortcut) |
m (→Oka and Uma) |
||
| (34 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
At the end of the game, the [[scoring|raw scores]] are converted into an "end game score". | At the end of the game, the [[scoring|raw scores]] are converted into an "end game score". This is most commonly referred as the plus-minus (+/-) score. The four end game scores are always set up to sum to zero. | ||
==Oka and | ==Oka and Uma== | ||
After the game ends, oka and uma are applied. | |||
The ''' | ===Oka=== | ||
The '''oka''' {{kana|オカ}} can be thought of as an "ante". When oka is used, all players pay a set amount at the start of the game. At the end of the game, the sum is given to first place. This sum is known as the oka. | |||
The oka always is the difference between the starting score and target score. If the start score is 25,000 and the target score is 30,000, the difference would be 5k. Thus, every player would pay 5,000 points. Then, first place would receive (5,000 x 4) points back, for an oka of 20,000. Overall, first place has a net gain of 15,000 points, and the others lose 5,000 points. (The oka value would be stated as 20,000.) | |||
If oka is disabled, then even if a target score is set, no payments are made. | |||
===Uma=== | |||
The '''uma''' {{kana|ウマ}} is a set bonus/penalty for ending the game at a certain placement. The typical point spread uses the format of {{uma|+A|+B|-B|-A}}, where 1st place receives A, 2nd receives B, 3rd loses B, and 4th loses A. | |||
The uma does not have to be symmetric. For example, uma can be set to {{uma|+30|-5|-10|-15}} or {{uma|+15|-5|-5|-5}}. Uma usually adds up to 0, but technically does not have to. Modifications may be used to make the conditions easier or harder, namely in tournament settings. | |||
==Procedure== | ==Procedure== | ||
[[Image:PlusMinus.png|thumb|240px|right|End game results with raw scores and uma scores]] | |||
The end game score is calculated as follows: | The end game score is calculated as follows: | ||
# | # Take the raw scores from the end of the game. | ||
# Subtract the target score from the final point values. (If no oka is used, subtract the starting score instead.) | |||
# Subtract the target score from the final point values. | # Find the '''oka''' and add it to the winner. | ||
# | |||
# Divide by 1,000. | # Divide by 1,000. | ||
# Round to the nearest integer. | # Round to the nearest integer. A result of 0.5 is rounded down, not up. | ||
# Apply the ''uma'' spread | # Apply the ''uma'' spread. | ||
# If the sum of all four does not equal to zero, then the winner's score is adjusted to produce a zero sum. | # If, due to rounding, the sum of all four does not equal to zero, then the winner's score is adjusted to produce a zero sum. This adjustment is usually +/- 1 at most. (Note: in some rules, the loser's score may be adjusted instead.) | ||
Formula: | |||
End score = ((Raw points + Oka - Target)/1000) + Uma | |||
===Shortcut=== | ===Shortcut=== | ||
For a given value of oka and uma, the overall change between raw score and final score will be the same. Therefore, by finding the net change from oka/uma once, you can skip having to do the entire process over and over. | |||
This | |||
#Before playing, calculate <code>Final Score - (raw score / 1000)</code> for each place. Use dummy numbers for raw score. | |||
#After finishing the game, find the raw score, round it to the nearest 1,000 (rounding 500 down), then divide by 1,000. | |||
#Use the calculated values from #1 to quickly determine final scores. | |||
For example, if all players ended with 25,000 points, oka = 20k, and uma = {{uma|+20|+10|-10|-20}}: | |||
{{uma compare| | |||
<!--player scores--> | |||
|score1 = 25000 | |||
|score2 = 25000 | |||
|score3 = 25000 | |||
|score4 = 25000 | |||
<!--uma settings--> | |||
|uma1 = 20 | |||
|uma2 = 10 | |||
|uma3 = -10 | |||
|uma4 = -20 | |||
|startpts = 25000 | |||
|targetpts = 30000 | |||
}} | |||
This means, for these oka/uma settings, 1st place final score is equal to <code>(rounded raw score/1000) + 10</code>, 2nd place final score is equal to <code>(rounded raw score/1000) - 20</code>, and so on. In other words: instead of having to calculate oka and uma every single time, when you are 1st with these settings, you can divide score by 1000, then add 10. | |||
Using the above picture as another example: | |||
{{uma compare| | |||
<!--player scores--> | |||
|score1 = 35700 | |||
|score2 = 32400 | |||
|score3 = 22200 | |||
|score4 = 9700 | |||
<!--uma settings--> | |||
|uma1 = 20 | |||
|uma2 = 10 | |||
|uma3 = -10 | |||
|uma4 = -20 | |||
|startpts = 25000 | |||
|targetpts = 30000 | |||
}} | |||
First place received 35700 points, so their end score equals <code>(36000) / 1000 + 10</code> = 46, which is what what first place actually got. | |||
===With different oka and uma=== | |||
Naturally, with different oka and uma settings, the numbers will work themselves out differently than the {{uma}} set up. | |||
With an uma of {{Uma|30|15|-15|-30}}: | |||
{{uma compare| | |||
<!--player scores--> | |||
|score1 = 35700 | |||
|score2 = 32400 | |||
|scpre3 = 22000 | |||
|score4 = 9700 | |||
<!--uma settings--> | |||
|uma1 = 30 | |||
|uma2 = 15 | |||
|uma3 = -15 | |||
|uma4 = -30 | |||
|startpts = 25000 | |||
|targetpts = 30000 | |||
}} | |||
Obviously, the net change is different. | |||
== Tie-breaker == | == Tie-breaker == | ||
[[Image:Tiedscores.png|thumb|240px|right|End game results with two players with the [http://tenhou.net/0/?log=2014011412gm-0009-7447-f4a2bbb5&tw=1 same raw scores].]] | [[Image:Tiedscores.png|thumb|240px|right|End game results with two players with the [http://tenhou.net/0/?log=2014011412gm-0009-7447-f4a2bbb5&tw=1 same raw scores].]] | ||
When scores are tied, there are two main variations to how it is handled: | |||
* Ties are broken based on the initial [[Jikaze|wind seating]] (seats in the first hand). When scores are tied, the initial East player beats South beats West beats North. | |||
* Tied players split oka/uma bonuses evenly. For example, with an uma of {{Uma|20|10|-10|-20}}, if two players tie for 3rd, they would pay (-10 + -20) / 2 = -15 each. | |||
Which variation is used will depend on the ruleset. | |||
== Competition formats == | |||
{{main|Multi hanchan format}} | |||
For some competitions, the same four players play out two or more hanchan to settle a score. This is due to one hanchan deemed as inadequate to settle a score between four players due to factors such as luck. Various tournaments and professional organizations use this format. | |||
==External links== | ==External links== | ||
Revision as of 17:32, 22 August 2024
At the end of the game, the raw scores are converted into an "end game score". This is most commonly referred as the plus-minus (+/-) score. The four end game scores are always set up to sum to zero.
Oka and Uma
After the game ends, oka and uma are applied.
Oka
The oka 「オカ」 can be thought of as an "ante". When oka is used, all players pay a set amount at the start of the game. At the end of the game, the sum is given to first place. This sum is known as the oka.
The oka always is the difference between the starting score and target score. If the start score is 25,000 and the target score is 30,000, the difference would be 5k. Thus, every player would pay 5,000 points. Then, first place would receive (5,000 x 4) points back, for an oka of 20,000. Overall, first place has a net gain of 15,000 points, and the others lose 5,000 points. (The oka value would be stated as 20,000.)
If oka is disabled, then even if a target score is set, no payments are made.
Uma
The uma 「ウマ」 is a set bonus/penalty for ending the game at a certain placement. The typical point spread uses the format of 「+A / +B / -B / -A」, where 1st place receives A, 2nd receives B, 3rd loses B, and 4th loses A.
The uma does not have to be symmetric. For example, uma can be set to 「+30 / -5 / -10 / -15」 or 「+15 / -5 / -5 / -5」. Uma usually adds up to 0, but technically does not have to. Modifications may be used to make the conditions easier or harder, namely in tournament settings.
Procedure
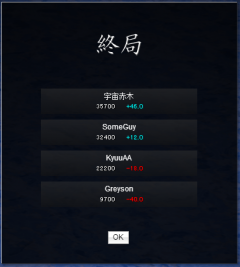
The end game score is calculated as follows:
- Take the raw scores from the end of the game.
- Subtract the target score from the final point values. (If no oka is used, subtract the starting score instead.)
- Find the oka and add it to the winner.
- Divide by 1,000.
- Round to the nearest integer. A result of 0.5 is rounded down, not up.
- Apply the uma spread.
- If, due to rounding, the sum of all four does not equal to zero, then the winner's score is adjusted to produce a zero sum. This adjustment is usually +/- 1 at most. (Note: in some rules, the loser's score may be adjusted instead.)
Formula:
End score = ((Raw points + Oka - Target)/1000) + Uma
Shortcut
For a given value of oka and uma, the overall change between raw score and final score will be the same. Therefore, by finding the net change from oka/uma once, you can skip having to do the entire process over and over.
- Before playing, calculate
Final Score - (raw score / 1000)for each place. Use dummy numbers for raw score. - After finishing the game, find the raw score, round it to the nearest 1,000 (rounding 500 down), then divide by 1,000.
- Use the calculated values from #1 to quickly determine final scores.
For example, if all players ended with 25,000 points, oka = 20k, and uma = 「+20 / +10 / -10 / -20」:
| Raw score conversion | Score comparison: Uma 「20 / 10 / -10 / -20」 | ||||
|---|---|---|---|---|---|
| Raw scores | Rounded to nearest 1000 | Div by 1000 (A) | End score (B) | End score diff (B - A) | |
| 25000 | 25000 | 25 | 35 | 10 | |
| 25000 | 25000 | 25 | 5 | -20 | |
| 25000 | 25000 | 25 | -15 | -40 | |
| 25000 | 25000 | 25 | -25 | -50 | |
This means, for these oka/uma settings, 1st place final score is equal to (rounded raw score/1000) + 10, 2nd place final score is equal to (rounded raw score/1000) - 20, and so on. In other words: instead of having to calculate oka and uma every single time, when you are 1st with these settings, you can divide score by 1000, then add 10.
Using the above picture as another example:
| Raw score conversion | Score comparison: Uma 「20 / 10 / -10 / -20」 | ||||
|---|---|---|---|---|---|
| Raw scores | Rounded to nearest 1000 | Div by 1000 (A) | End score (B) | End score diff (B - A) | |
| 35700 | 36000 | 36 | 46 | 10 | |
| 32400 | 32000 | 32 | 12 | -20 | |
| 22200 | 22000 | 22 | -18 | -40 | |
| 9700 | 10000 | 10 | -40 | -50 | |
First place received 35700 points, so their end score equals (36000) / 1000 + 10 = 46, which is what what first place actually got.
With different oka and uma
Naturally, with different oka and uma settings, the numbers will work themselves out differently than the 「+20 / +10 / -10 / -20」 set up.
With an uma of 「30 / 15 / -15 / -30」:
| Raw score conversion | Score comparison: Uma 「30 / 15 / -15 / -30」 | ||||
|---|---|---|---|---|---|
| Raw scores | Rounded to nearest 1000 | Div by 1000 (A) | End score (B) | End score diff (B - A) | |
| 35700 | 36000 | 36 | 56 | 20 | |
| 32400 | 32000 | 32 | 17 | -15 | |
| 30000 | 25000 | 25 | -20 | -45 | |
| 9700 | 10000 | 10 | -50 | -60 | |
Obviously, the net change is different.
Tie-breaker
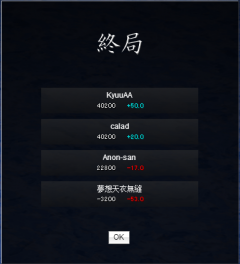
When scores are tied, there are two main variations to how it is handled:
- Ties are broken based on the initial wind seating (seats in the first hand). When scores are tied, the initial East player beats South beats West beats North.
- Tied players split oka/uma bonuses evenly. For example, with an uma of 「20 / 10 / -10 / -20」, if two players tie for 3rd, they would pay (-10 + -20) / 2 = -15 each.
Which variation is used will depend on the ruleset.
Competition formats
For some competitions, the same four players play out two or more hanchan to settle a score. This is due to one hanchan deemed as inadequate to settle a score between four players due to factors such as luck. Various tournaments and professional organizations use this format.
External links
- Oka and uma in Japanese Wikipedia