Oka and uma: Difference between revisions
m (→Shortcut) |
|||
| Line 21: | Line 21: | ||
This short cut only applies to the distribution of (+20/+10/-10/-20). Using the procedure above, suppose all players unrealistically finish with 25,000 points each. The target points is 30,000 as standard. | This short cut only applies to the distribution of (+20/+10/-10/-20). Using the procedure above, suppose all players unrealistically finish with 25,000 points each. The target points is 30,000 as standard. | ||
{| class="wikitable" | {| class="wikitable" width=60% | ||
|- | |- | ||
! End points !! Oka !! Minus target !! Add oka !! Div 1000 !! Rounded !! +/- !! End score !! Diff. from start | ! End points !! Oka !! Minus target !! Add oka !! Div 1000 !! Rounded !! +/- !! End score !! Diff. from start | ||
| Line 38: | Line 38: | ||
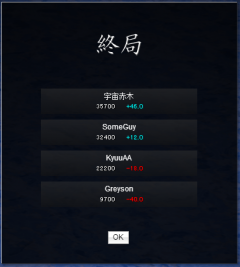
Just to show, the values in the image to the right are used: | Just to show, the values in the image to the right are used: | ||
{| class="wikitable" | {| class="wikitable" width=60% | ||
|- | |- | ||
! End points !! Oka !! Minus target !! Add oka !! Div 1000 !! Rounded !! +/- !! End score !! Diff. from start | ! End points !! Oka !! Minus target !! Add oka !! Div 1000 !! Rounded !! +/- !! End score !! Diff. from start | ||
Revision as of 08:29, 23 August 2013
Uma is the end game adjusted score. This is most commonly referred as the plus-minus (+/-) score.
Oka
The oka is the point difference between the start score and the target score; and then it is multiplied by the number of players. In general, this can be viewed as the "ante". Typically, the start score and target score are 25,000 pts and 30,000 pts respectively. So, in this case the oka is 5,000 x 4.
Procedure
The end game score is calculated as follows:
- Raw are taken at the end of the game, naturally ordered by the final point values.
- Note the start score and target score point difference, find the oka.
- Subtract the target score from the final point values.
- Add the oka to the winner.
- Divide by 1,000.
- Round to the nearest integer. If the division result produces a digit of 0.5, then the number is rounded down.
- Apply the uma spread, if any.
- If the sum of all four does not equal to zero, then the winner's score is adjusted to produce a zero sum.
Due to rounding, the final values may not add up to zero. Therefore, it may become necessary to alter the winner's score. Usually, the difference is only +/- 1.
Shortcut
This short cut only applies to the distribution of (+20/+10/-10/-20). Using the procedure above, suppose all players unrealistically finish with 25,000 points each. The target points is 30,000 as standard.
| End points | Oka | Minus target | Add oka | Div 1000 | Rounded | +/- | End score | Diff. from start |
|---|---|---|---|---|---|---|---|---|
| 25000 | 20000 | -5000 | 15000 | 15 | 15 | +20 | 35 | +10 |
| 25000 | 0 | -5000 | -5000 | -5 | -5 | +10 | 5 | -20 |
| 25000 | 0 | -5000 | -5000 | -5 | -5 | -10 | -15 | -40 |
| 25000 | 0 | -5000 | -5000 | -5 | -5 | -20 | -25 | -50 |
As a shortcut, the adjustment can use the scores in the first column. Then the scores can be divided by 1000 and rounded. Finally, the values in the last column can be used to adjust for the final scores. Once again, this only works with the regular (+20/+10/-10/-20) uma.
Just to show, the values in the image to the right are used:
| End points | Oka | Minus target | Add oka | Div 1000 | Rounded | +/- | End score | Diff. from start |
|---|---|---|---|---|---|---|---|---|
| 35700 | 20000 | 5700 | 25700 | 25.7 | 26 | +20 | +46 | +10 |
| 32400 | 0 | 2400 | 2400 | 2.4 | 2 | +10 | +12 | -20 |
| 22200 | 0 | -7800 | -7800 | -7.8 | -8 | -10 | -18 | -40 |
| 9700 | 0 | -20300 | -20300 | -20.3 | -20 | -20 | -40 | -50 |
If the original scores of (35700, 32400, 22200, 9700) were rounded and divided by 1000, the original scores would be converted to (36, 32, 22, 10). If (+10, -20, -40, -50) were added to the converted numbers, they would produce (46, 12, -18, -40).